Generate curl noise

One of the use cases for fractal noise is to simulate natural phenomena. perlin/simplex noise are e.g. often used to create flow fields, but this can be problematic as they are not divergence-free (particles will concentrate at sinks/gutters in the field). An approach to avoid this is to take the curl of a field instead. The curl operator is ensured to produce divergence-free output, when supplied with continuous fields such as those generated by simplex and perlin noise. The end result is a field that is incompressible, thus modelling fluid dynamics quite well.

curl_noise(
  generator,
  x,
  y,
  z = NULL,
  ...,
  seed = NULL,
  delta = NULL,
  mod = NULL
)

Arguments

generator: The noise generating function, such as gen_simplex, or fracture()
x, y, z: The coordinates to generate the curl for as unquoted expressions
...: Further arguments to generator
seed: A seed for the generator. For 2D curl the seed is a single integer and for 3D curl it must be a vector of 3 integers. If NULL the seeds will be random.
delta: The offset to use for the partial derivative of the generator. If NULL, it will be set as 1e-4 of the largest range of the dimensions.
mod: A modification function taking the coordinates along with the output of the generator call and allow modifications of it prior to calculating the curl. The function will get the coordinates as well as a value holding the generator output for each coordinate. If the curl is requested in 2D the value will be a numeric vector and mod() should return a numeric vector of the same length. IF the curl is requested in 3D the value is a list of three numeric vectors (x, y, and z) and mod() should return a list of three vectors of the same length. Passing NULL will use the generator values unmodified.

References

Bridson, Robert. Hourihan, Jim. Nordenstam, Marcus (2007). Curl-noise for procedural fluid flow. ACM Transactions on Graphics 26(3): 46. doi:10.1145/1275808.1276435.

Examples

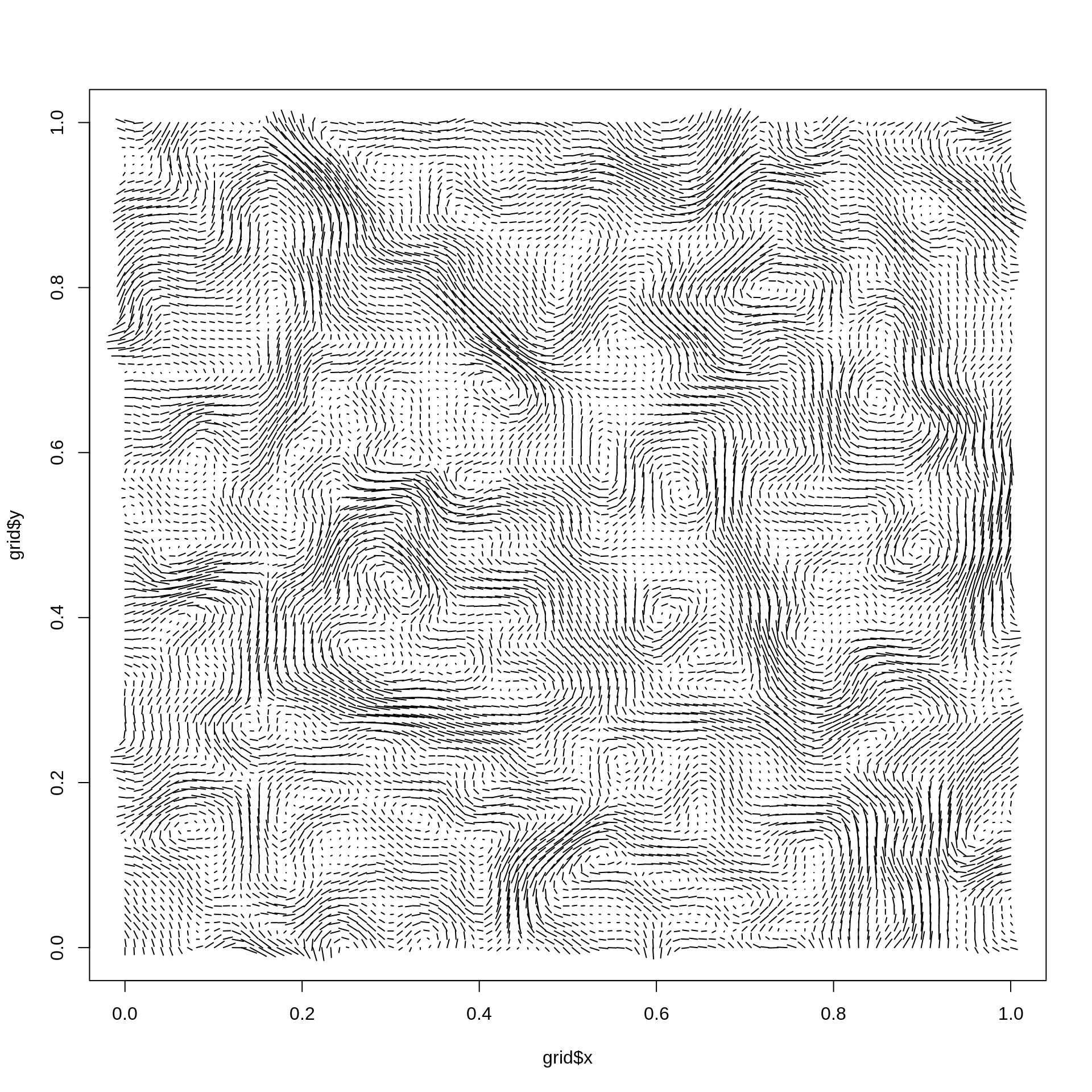
grid <- long_grid(seq(0, 1, l = 100), seq(0, 1, l = 100))

# Use one of the generators
grid$curl <- curl_noise(gen_simplex, x = grid$x, y = grid$y)
plot(grid$x, grid$y, type = 'n')
segments(grid$x, grid$y, grid$x + grid$curl$x / 100, grid$y + grid$curl$y / 100)


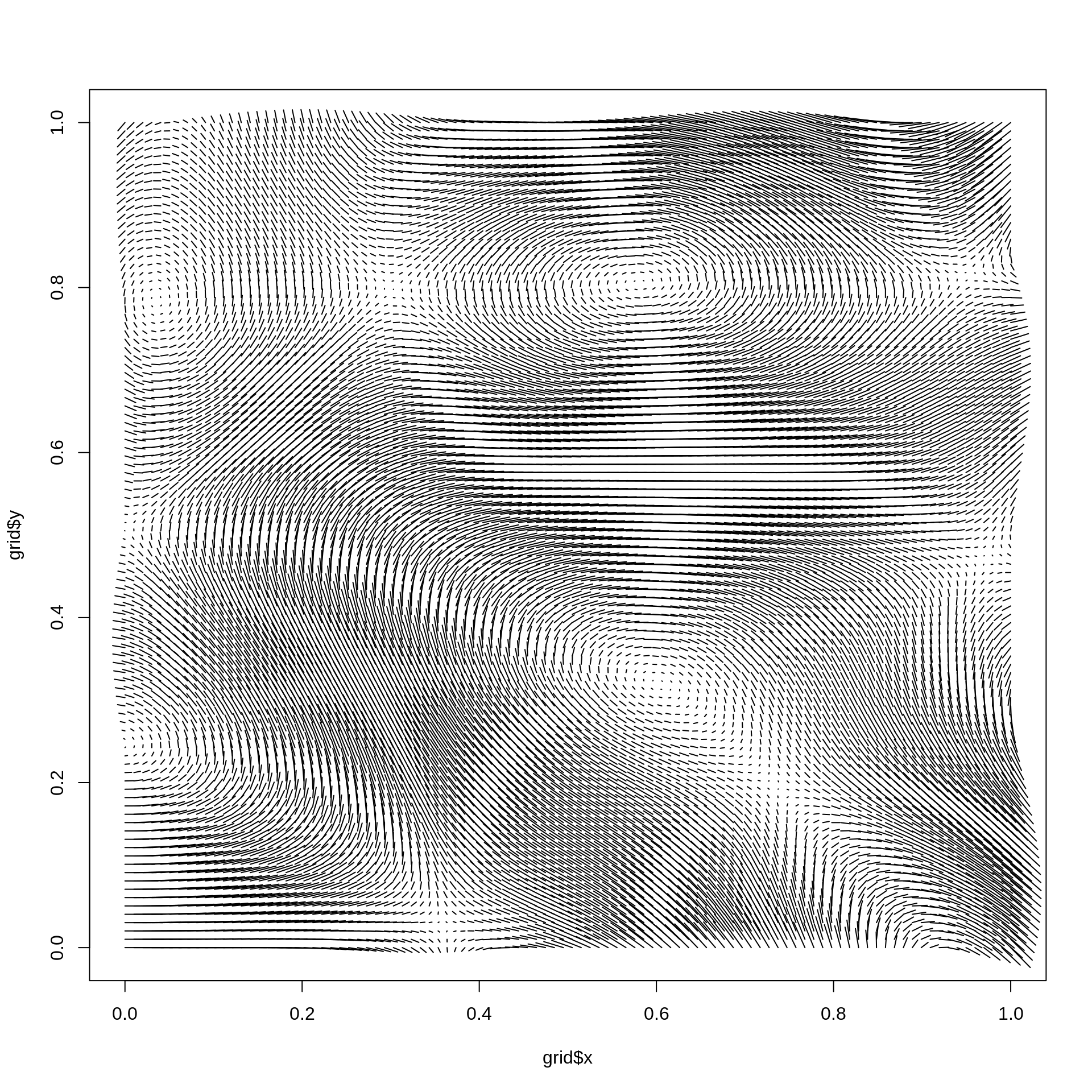# If the curl of fractal noise is needed, pass in `fracture` instead
grid$curl <- curl_noise(fracture, x = grid$x, y = grid$y, noise = gen_simplex,
                        fractal = fbm, octaves = 4)
plot(grid$x, grid$y, type = 'n')
segments(grid$x, grid$y, grid$x + grid$curl$x / 500, grid$y + grid$curl$y / 500)

Arguments

References

See also

Examples